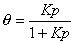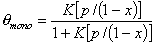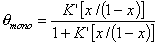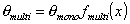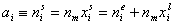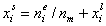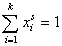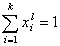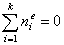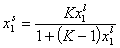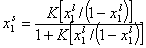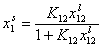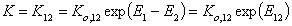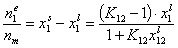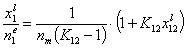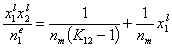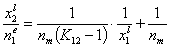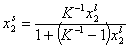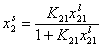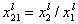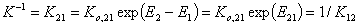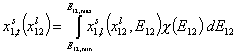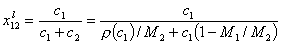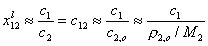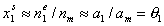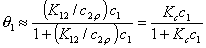© A.W.Marczewski 2002

A Practical Guide to Isotherms of ADSORPTION on Heterogeneous Surfaces

Reload Adsorption Guide

Basics of Adsorption on Solids

NOTE. This short document is not a complete description of the problem (see e.g. note below). If the reader wants a more profound and complete study of the basic definitions used in adsorption, please consult e.g. one of the sources, and especially this short monograph:
J. Oscik, "Adsorption", PWN Warsaw - Ellis Horwood Ltd., Publishers, Chichester 1982
See also my Adsorption Glossary

Gases, liquid mixtures and dilute solutions
Gas ( Basics )
Non-electrolyte liquids ( Basics, Everett iso., linear plots, heterogeneity )
Dilute solutions ( Dilute solutions )

Measured quantity:

In adsorption, the measurable quantity is always a so called adsorption excess (or Gibbs adsorption), whereas most theories of adsorption deal with adsorbed amount (called just adsorption value or absolute adsorption) - see below. However, in some cases - namely for gas or dilute solute adsorption - we may simplify considerations and assume that the measured quantity (excess) is the same as adsorbed amount. This assumption seems quite straightforward for gas adsorption, but it is not obvious for dilute solute adsorption.

Basics of gas adsorption:

First, lets consider gas adsorption:
Measured quantity is surface excess - practically equal to true adsorption, a.
NOTE. It is due to typically low concentrations of gases in gas phase (use Ideal Gas Law: c = n/v and pv = nRT, thus c = p/RT; at standard conditions the sum of molar concentations of all gases is approx. 0.045 mol/dm³). In order to compare densities of surface and gas phase one may use densities of gas phase and adsorbed (i.e. condensed) phase. E.g. for N₂ at standard conditions ρ_gas / ρ_ads ≈ 1.3g/dm³ / 0.8g/cm³ ≈ 2·10^-3.

For ideal both phases - no lateral interactions, homogeneous surface:
Adsorption isotherm: Langmuir eqn.:

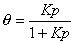
Monolayer part of multilayer adsorption of vapour (gas below critical point):

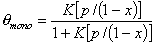
or

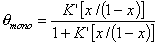
where x = p/p_s and K' = K p_s and

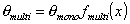
where the form of f_multi(x) depends on the multilayer formation model as well as the available space (infinite no. of layers only for flat adsorbent space, for macro- and mesoporous solids the space - and no. of layers must be limited). The most often used model is BET equation with quite simple multilayer factor.

Basics of liquid adsorption:

NOTE. In the following it is assumed for simplicity, that the molecular sizes (and molecular volumes) are identical or similar. Otherwise the sum of n_i^s may not be constant and equal to n_m^s as it is implied below. In such a case, though the total occupied surface area is constant, the no. of molecules in adsorption space and corresponding surface phase volume will depend on cross-sectional area and - for non-spherical molecules - orientation of molecules. For adsorption in smaller pores, where the adsorption space has constant volume, the preferred way to deal with the problem may be using volume fractions instead of molar fractions.
See: J. Oscik, "Adsorption", PWN Warsaw - Ellis Horwood Ltd., Publishers, Chichester 1982.

Now, lets look at binary liquid adsorption:
Measured quantity: surface excess, n_i^e related to true adsorption n_i^s (or a_i) by following dependences (symmetrical with respect to component exchange):

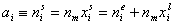
or

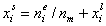
where superscript "l" denotes liquid, "s" surface phase, x_i is molar fraction of component "i", n^s is adsorption (n_i^s) and n^e is surface excess (n_i^e) being the total excess of component "i" in surface phase vs. bulk phase per amount of adsorbent (or adsorbent surface).

The model picture (click to enlarge) shows an example of concentration profile C(x) of component "i" vs. distance from surface, and concentration (extrapolated to the surface) in the bulk phase (C_bulk). The shaded area corresponds to the adsorption excess.

For any multicomponent system we always have by definition :

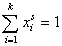
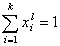
and (for equal molecular sizes - see note):

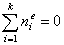
For ideal both phases - no lateral interactions, homogeneous surface - the composition of a surface phase for a binary liquid system in contact with solid surface is given by a classic Everett isotherm equation (being a simple analogue of Langmuir equation), where the components are interchangeable (i.e. "1" may be exchanged to "2") without change of eq. form:
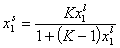(Everett isotherm)
By simple rearrangement we get:

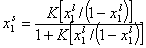
This eqn. describes competition of components "1" and "2". Thus, we may rewrite this as an equation formally identical with Langmuir equation (if we put p = x₁₂^l and K = K₁₂):

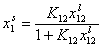
where
and

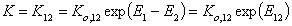
If we use measured quantity, i.e. surface excess n_i^e , instead of surface mole fractions x_i^s, we will get for component "1":

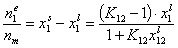
This equation may be easily transformed into several linear forms, analogues of Langmuir or BET linear plots (2^nd eq. is often used in order to estimate surface phase capacity and is also known as Everett linear plot or just Everett iso. equation - most often n^s is used instead of n_m) :

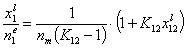
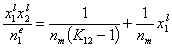(Everett linear plot)
and

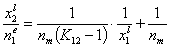
Analogously, by simple rearrangement of original Everett eqn. for component "1", we will obtain isotherm equation for component "2" :

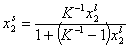
and we may rewrite this

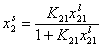
where
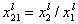and

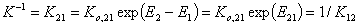
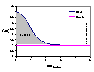
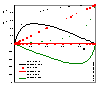
The picture (click to enlarge) shows comparison of surface excess, n₁^e (solid lines) and respective adsorption n₁^s values (dotted lines) for model Everett isotherm (homogeneous surface, ideal surface and bulk phase) and 3 values of adsorption constant K₁₂ = K₁ / K₂ : 10 (stronger adsorption of "1" - positive excess of "1"), 1 (equal adsorption properties of "1" and "2" - adsorption excess is 0 everywhere) and 0.1 (stronger adsorption of "2" - negative excess of "1" and positive excess of "2")

Thus for adsorption in binary liquid mixtures we obtain general integral equation (see general discussion and compare single gas and dilute solute adsorption, binary liquid mixtures and multicomponent adsorption):

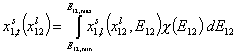
where subscript "t" denotes global adsorption and "l" local isotherm (i.e. Everett eqn. or other isotherm including eg. lateral interactions etc.) and χ(E₁₂) is the distribution of adsorption energy differences E_ij=E_i-E_j.

We may use similarity of form of general integral equations (for appropriately formulated isotherm) for liquids and gases to find, that in such a case it is enough to replace gas pressure "p" by ratio of molar fractions in binary mixture to obtain respective isotherm for liquid adsorption. Then energy of gas adsorption E is replaced by the difference of adsorption energies of components "1" and "2" and distribution function of adsorption energy E is replaced by distribution of energy differences. I

Basics of dilute solute adsorption:

We may try to simplify respective equations for liquid mixtures by changing molar fractions to molar concentrations, most often used to express solute concentration in dilute solutions:

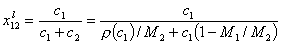
where c_i is molar concentration, ρ is solution density, M_i is molar mass.
Then, for dilute solution c₁ << c₂ (if "1" is solute and "2" is solvent, e.g. water):

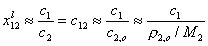
where ρ_2,o = ρ(c₁=0) (density of pure solvent) and c_2,o is molar concentration of solvent in pure solvent (e.g. for water c_water = 55mol/dm³).
At the same time x₁^l << x₂^l, and:

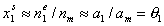
(for monolayer adsorption, monolayer capacity a_m is the same as surface phase capacity n_m).
Then, after substitution of x₁₂^l and x₁^s into the Everett equation we get a good approximation identical in form with the Langmuir isotherm for gas adsorption:

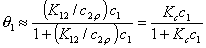
where K_c = K₁₂/c_2,o and K₁₂ = K_o,12 exp(E₁₂).

Top

Send a message to Adam.Marczewski AT@AT umcs.lublin.pl

Disclaimer